Overview
Our project integrated computational modeling at every stage, from initial design to final system validation. We began with Internal Modeling to shape our project's design, and this foundational work led to the development of our primary contribution: a powerful, outward-facing External Modeling pipeline designed to quantify and predict the dynamics of engineered biological systems, which we present as a reusable tool for the iGEM community.
Brainstorming/Development Process
Our Dry Lab creation process was one filled with constant shifts in ideas. We started the season believing we would be 3D-modeling healing cracks in concrete, as well as exploring finite element modeling (which engineers use to simulate bridges collapsing). Then, with input from one of our mentors, Chris and his colleague JJ Yeo at Cornell who works on models like these, he advised us to focus on the chemistry on our project first, suggesting an Ordinary Differential Equation (ODE) model first. As such, we adjusted the scope and goals of our Dry Lab to creating the ODE and ensuring we were integrated with and useful to our Wet Lab.
Part 1: Internal Modeling
Foundational Work to Guide Our Project
To accelerate our project's design phase, we used a suite of in-silico tools to make critical decisions before beginning wet lab work. This approach allowed us to evaluate potential candidates, rule out non-viable paths, and accelerate our conceptualization process, saving valuable time and resources.
From Sequence to Structure to Prototype
Our initial challenge was selecting a core protein for our system. We performed a rapid computational screen on several candidates using tools like ProtParam to evaluate key biochemical properties (isoelectric point, acidic residue content, stability). This allowed us to quickly compare proteins based on their predicted suitability for biomineralization. While this analysis pointed to the CARP protein as a strong candidate, we ultimately proceeded with an engineered CsgA construct. The true value of this exercise was in rapidly accelerating our conceptualization and establishing a data-driven workflow early on.
With our design direction focused, we used AlphaFold to predict the 3D structure of our engineered protein. The model revealed that our modifications could lead to the formation of a novel pore-like oligomer instead of a standard amyloid fiber, a key structural insight.

Finally, we used computer-aided design (CAD) software to design the physical hardware for our system. This digital blueprint was then used to 3D print a high-resolution mold, which we in turn used to cast the final device from Polydimethylsiloxane (PDMS), a biocompatible polymer. This demonstrates our engineering cycle, moving from a digital model to a physical prototype.

External: Reusable Modeling Pipeline for Future Teams
To quantify and predict the performance of our system, we developed a comprehensive software pipeline. This tool automates the entire workflow from raw experimental data to a sophisticated system simulation with uncertainty analysis, and we have packaged it as a robust, reusable tool for the iGEM community.
The Three-Stage Analysis Pipeline
Our tool transforms raw data into a predictive simulation in three automated stages:
- Stage 1 (assay): It processes dual-wavelength spectrophotometer absorbance traces (≈560/435 nm) by converting them to pH via the phenol-red ratio and the Henderson–Hasselbalch relationship, identifies an early linear window, and calculates the initial reaction rate \( v_{0} \) along with a data quality score \( R^2 \).
- Stage 2 (fit): We aggregate per-run initial rates \( v_{0} \) from Stage 1 and pair each with its corresponding substrate concentration (([S])) from run_meta.csv. For each enzyme, we fit the Michaelis–Menten model
by nonlinear least squares whenever at least three distinct substrate concentrations are available. To quantify uncertainty, we bootstrap the dataset (resampling runs with replacement, refitting (n = 500) times) and record the parameter distributions,reporting the mean, bootstrap standard error, and 5–95 % confidence intervals.
If fewer than three unique substrate concentrations are available, we use the fallback one_point_fixed_Km method: \( K_{m} \) is fixed to a literature value (e.g., 9.3 mM for CA) and \( V_{\max} \) is estimated analytically from the available points, still with bootstrap uncertainty.
Each enzyme’s output is written automatically to results/kinetics_
.json for the user. These fitted parameter distributions feed Stage 3, where the ODE simulator samples \( V_{\max} \),Km to produce personalized predictions with uncertainty bands. \( v = \frac{V_{\max}[S]}{K_m + [S]} \)
- Stage 3 (simulate): It uses these experimentally-derived parameters to power a system of Ordinary Differential Equations (ODEs) that forecasts the system's behavior over time.
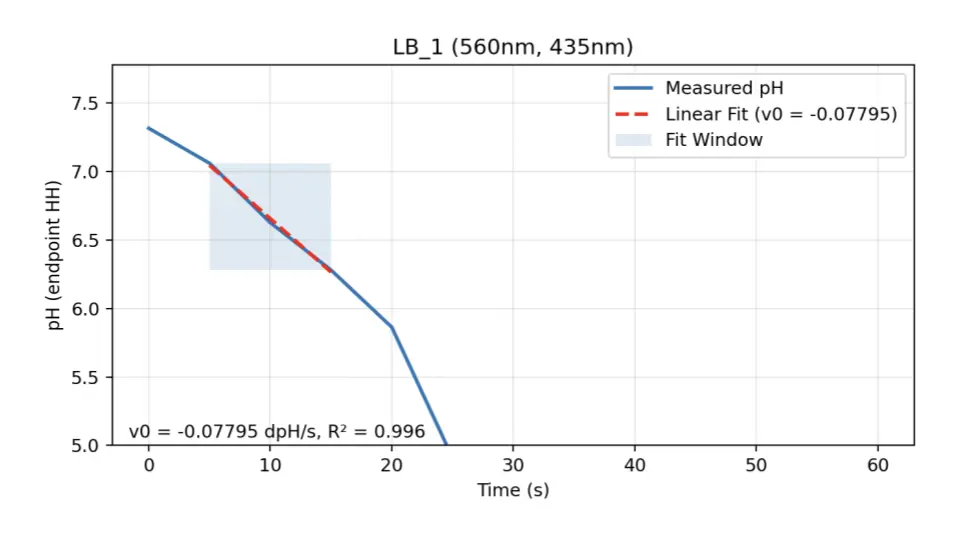
Methods (dual-λ → pH → (\( v_{0} \)))
Ratio: \( R = \dfrac{A_{560}}{A_{435}} \) with endpoints \( (R_{\text{acid}}, R_{\text{base}}) \).
pH transform: \( \mathrm{pH} = pK_a' + \log_{10}\!\left(\dfrac{R - R_{\text{acid}}}{R_{\text{base}} - R}\right) \).
Early rate: \( v_0 = \dfrac{d\,\mathrm{pH}}{dt} \) (linear fit on the first \( t \) seconds; we report \( R^2 \)).
Molar rate: \( v_0^{\text{molar}} = \beta \cdot \dfrac{d\,\mathrm{pH}}{dt} \) (buffer capacity \( \beta \)).
Details & calibration in repo (params.py, assay_v0.py).
A Deep Dive into the ODE Model
The behavior of the system is described by the following set of coupled differential equations:
\( C_{\text{carb}} \) (mM):
The concentration of dissolved carbonate.\( C_{\text{CaCO3}} \)
The concentration of precipitated calcium carbonate.\( X \)
The density of viable, productive cells.
The core of our pipeline is a predictive ODE model that simulates the dynamics of biomineralization. The model tracks three key state variables:
\[ \begin{aligned} \frac{dC_{\text{carb}}}{dt} &= r_{\text{prod}} - r_{\text{precip}} \\ \frac{dC_{\text{CaCO3}}}{dt} &= r_{\text{precip}} \\ \frac{dX}{dt} &= \mu_{\text{max}} \cdot \mathrm{burden}(r_{\text{prod}}, V_{\max}) \cdot X \end{aligned} \]
Breaking down each component
- Carbonate Production \( r_{\text{prod}} \)
- CaCO₃ Precipitation \( r_{\text{precip}} \):
The precipitation of calcium carbonate from solution is modeled using second-order kinetics, dependent on the concentration of both the dissolved carbonate and the available free calcium ions in the media:
\( r_{\text{precip}} = k_{\text{precip}} \cdot [\text{Ca}^{2+}] \cdot C_{\text{carb}} \)
Assumptions & Boundary Conditions (for this version of the model)
- [Ca²⁺] treated as constant and in large excess. We do not deplete calcium in the ODE, so CaCO₃ can increase without a hard stoichiometric cap. This helps visualize kinetics, but in experiments precipitation is capped by the initial calcium pool.
- Substrate pool is lumped. For CA we treat the CO₂/HCO₃⁻/CO₃²⁻ system as an effective substrate [S] feeding \( r_{\text{prod}} \). Speciation is not explicitly modeled.
- Well-mixed, isothermal reactor with buffered pH (phenol-red assay).
- Simple nucleation/precipitation kinetics (second-order in ions); no nucleation lag or polymorph switching.
- Cell Growth and Metabolic Burden:
We moved beyond a simple exponential growth model to more realistically account for the energetic cost of producing our enzyme. The growth rate is modulated by a phenomenological burden factor:
\[ \text{burden factor} = \left(1 - b_0 - b_1 \cdot \frac{r_{\text{prod}}}{V_{\max}}\right)^{+} \]
This term dynamically penalizes the maximum growth rate (u_max) based on the cell's metabolic effort. As the enzyme's catalytic flux (r_prod) approaches its theoretical maximum (V_max), cellular resources are diverted, and growth slows. The parameters b0 and b1 represent the basal metabolic burden and the burden from catalytic activity, respectively.
The rate of dissolved carbonate production is driven by our engineered enzyme and is modeled using the Michaelis–Menten equation:
\[ r_{\text{prod}} = V_{\max} \cdot \frac{[S]}{K_m + [S]} \]
The parameters \( V_{\max} \) – the maximum reaction rate – and \( K_{m} \) (the substrate affinity) are not assumed; they are derived directly from our wet lab data in the fit stage of the pipeline.
Uncertainty Propagation and Model Predictions
A key feature of our model is its ability to quantify and propagate uncertainty. During the fit stage, we use bootstrapping to obtain parameter distributions for \( V_{\max} \) and \( K_{m} \) (from which we also report 5–95% confidence intervals). The simulate stage then runs hundreds of simulations, sampling from these bootstrap-derived parameter distributions (or perturbing point estimates when distributions are unavailable). The final output plots the mean prediction along with a shaded confidence interval, providing an honest and robust forecast of the system's likely performance range.

A Reusable Tool for iGEM
This entire pipeline is packaged as a user-friendly command-line tool designed for reproducibility. Every run generates a unique, timestamped folder containing all data, plots, parameters, and logs, ensuring that any result is fully traceable. We believe this tool represents a significant contribution that can help future iGEM teams bridge the gap between their wet lab data and predictive modeling.