Genetic circuit

Abstract

Pichia pastoris is a widely used host of microbial production systems. Regulable promoters, high yields, and reliable posttranslational modifications make it one of the most widely used yeasts for microbial production. Since it is a recognized system for recombinant protein production there have been efforts to improve it. In this section we present our proposal for 2 possible improvements to traditional P. pastoris production. The use of a license free strain from the Openpichia collection, and the use of a high expression regulable promoter PHpFMD. We use modeling to characterize these two components against traditional alternatives, the strain GS115 and the commonly used AOX1 promoter.

Introduction

Pichia pastoris has emerged as one of the most widely utilized microbial cell factories for recombinant protein production and bioprocessing applications. Its pervasive use in research and industry is attributable to a confluence of favorable genetic, metabolic, and process‐engineering characteristics that enable high yields, cost-effective cultivation, and production of proteins with complex post‐translational modifications (Cai et al., 2021; Chang et al., 2018; De et al., 2021; Irani et al., 2016; Vogl et al., 2016). Over the past several decades, advances in molecular biology and strain engineering have further augmented P. pastoris’s capabilities as a chassis for both academic and industrial applications, making it an attractive alternative to traditional hosts such as Escherichia coli and Saccharomyces cerevisiae (Cai et al., 2021; Claes et al., 2024; Vogl et al., 2016).

As part of its wider adoption in the field of synthetic biology it is necessary to develop well characterized, reliable, and versatile tools for the yeast. In this section we present 2 proposals for adoption as synthetic biology options. The first is one of the strains from OpenPichia, a license free expression system. The second is the use of an orthologous promoter HpFMD, which posses similar tunable expression as the standard AOX1, with the advantages of being able to function in the absence of methanol, and having higher expression under methanol (Claes et al., 2024; Vogl et al., 2020).

Methodology

Since our experimental section had some hurdles that prevented the full realization of the project, we are completing our information with other available studies on PHpFMD (Vogl et al., 2016, 2020). As for Openpichia we were able to perform basic experimental work, but conditions were not completely appropriate for modeling, so we are completing it with the original study in which the OpenPichia strains were reported (Claes et al., 2024).

Measuring growth

We measured growth of both OPENPichia pep4 yps1 and GS115 strains. They both grew in YPD medium on 250 ml flasks and under agitation. An Eppendorf BioPhotometer plus was used to measure optical density (OD) at 600 nm every hour for 6 hours, dilution was used as needed.

Model formulation

For growth we used a simple exponential growth model:

Where N is population or biomass as a function of time and measured by OD, N0 is the initial population, µ is the specific growth rate (h⁻¹), and t is time in hours. We linearize the equation using the natural logarithm of each side:

On which we can use linear regression to model our growth data.

Formulation of promoter dynamics

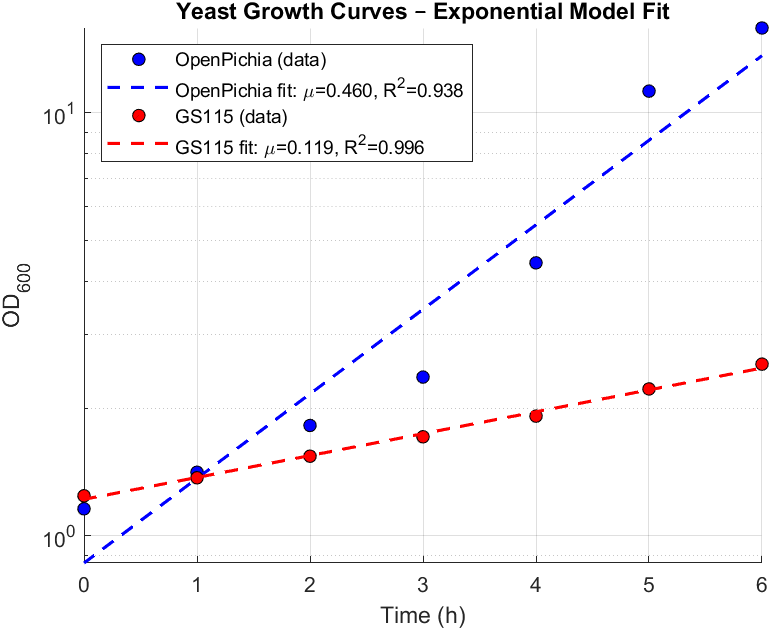
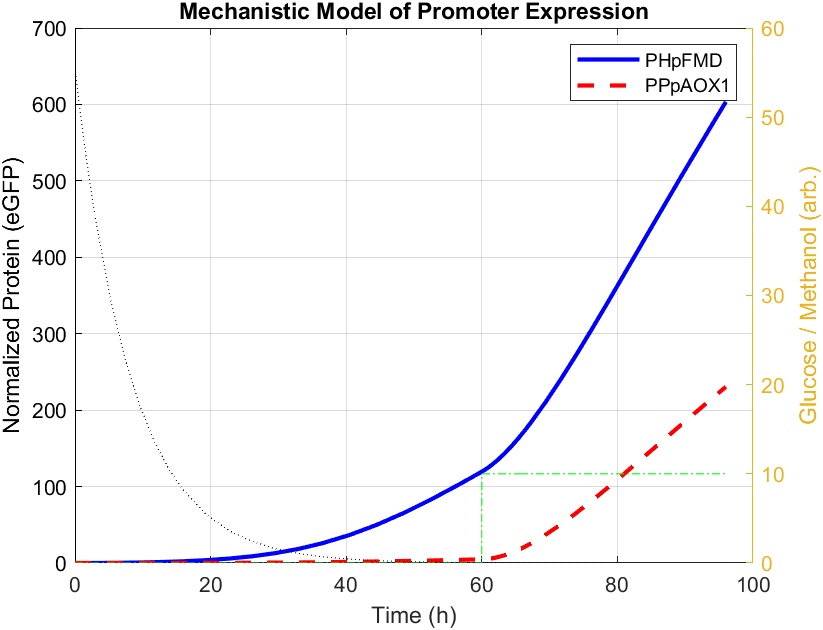
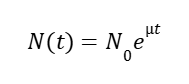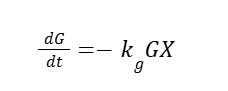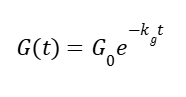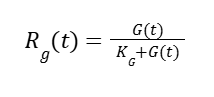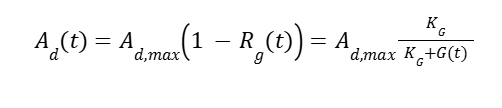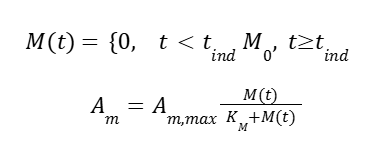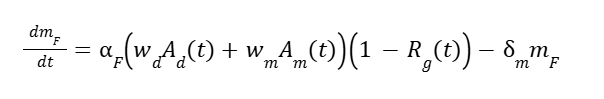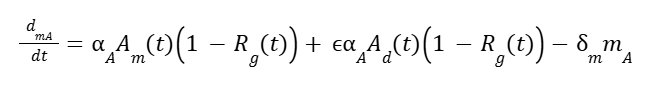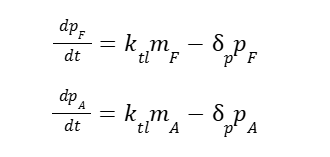We built a mechanistic ordinary differential equation (ODE) to represent the dynamics of both promoters HpFMD and AOX1. Both promoters are depressed by glucose, upon glucose depletion HpFMD shows strong derepressed activity, while AOX1 has very little expression until methanol is introduced. The formulation assumes that biomass is fixed. For glucose dynamics:

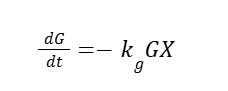
As glucose concentration (G, mM) is consumed in time t (h), where kg is the specific rate of consumption and X is biomass. Since we assume a normalize, steady biomass (X≈1):

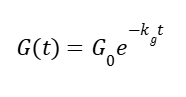
Where G0 is the initial concentration of glucose. Repressor activity is:

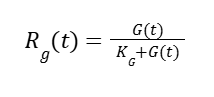
Where KG is the repression rate dependent on glucose. HpFMD has a strong de-repression activator in absence of glucose:

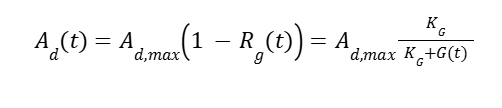
Where Ad is the de-repressor activator and Ad,max is the activator at maximum activity. Both are strongly induced under methanol added at induction time tind:

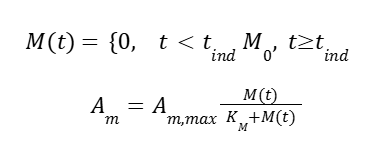
Where Am is the activity of the methanol induced activator, and KM is its specific rate. This leaves mRNA dynamics for HpFMD:

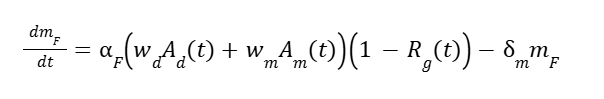
And for AOX1 is:

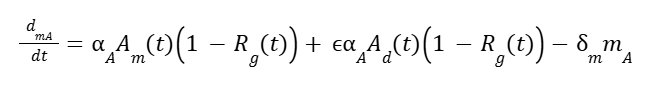
Where αF​ and αA​ are the max transcription rates, wd​ and wm​ are weights for de-repression vs methanol activation, ϵ is the weak de-repression factor for AOX1, m is mARN for AOX1 (A) and HpFMD (F), and δ is the degradation rate for mRNA

The protein dynamics for the same protein GFP (Vogl et al., 2020):

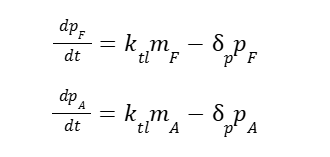
Where p is the protein production for AOX1 (A) and HpFMD (F).

We built both models in MATLAB R2023a.

Results and discussion

Growth model

As mentioned, the model was built using our own experimental data visible on table 1. It is important to mention that the GS115 was transformed to carry a plasmid (the strain was lent to us already transformed) while the OpenPichia strain was not transformed.

Table 1. Experimental data of the growth of both yeast strains measured by optical density.

As can be seen on table 1. The growth of the OpenPichia strain is considerably higher than that of GS115. It was previously reported that OpenPichia does have a higher µ than GS115, but the reported difference was not as high (Claes et al., 2024). We calculated that μ=0.44 (h−1) for OpenPichia and μ=0.12 (h−1) for GS115, with R2 values of 0.93 and 0.99 respectively, as can be seen in figure 1. OpenPichia has shown in the past to be as reliable as other strains of P. pastoris. Our results are in line with previous studies under similar conditions, the advantage of OpenPichia is in its reduced operating costs at industrial levels over other strains (Claes et al., 2024).

Expression models

We built our model based primarily based on the study by Vogl and colleagues from 2020. The parameters we used are available in supplementary information. As was the case in the study we obtained a high predicted production of protein by PHpFMD compared to AOX1. This high expression is caused both by the de-repression mechanism exhibited by the promoter and because of its higher induction by methanol. Since methanol is a toxic compound, there is persistent interest in eliminating it from production processes. The de-repressed expression is not as high as AOX1 under methanol so for either promoter the most attractive prospect is to continue to use methanol. The modeled behavior is in Figure 2. One of the attractive characteristics of AOX1 is its controllable expression. Pichia systems are often operated in 2 phases, one for growth without expression of the desired protein, and another with induced expression (Chang et al., 2018; De et al., 2021; Vogl et al., 2016). HpFMD offers another control tool for these systems since it works in 3 states, repression, de-repression, and induction. It could be used in genetic circuits as a tool for controllable expression or high yield of protein compared to AOX1.

Conclusion

The incremental development of new tools to enhance microbial production systems is important for the development of well characterized, robust, and reliable synthetic biology tools. OpenPichia as a license free production system, shows to not have significant differences with other strains. PHpFMD shows to be a potentially powerful tool for synthetic biology in yeasts, while orthologous promoters usually have poor performance in P. pastoris, this promoter shows the same option for controllable expression as AOX1 with higher production rates and the option for methanol free production.

On code availability

Code for both models is available on the software section of the project

Supplementary information: parameters used for the second model based on Volg et al, 2020

References

• Cai, P., Duan, X., Wu, X., Gao, L., Ye, M., & Zhou, Y. J. (2021). Recombination machinery engineering facilitates metabolic engineering of the industrial yeast Pichia pastoris. Nucleic Acids Research, 49(13), 7791–7805.
• Chang, C.-H., Hsiung, H.-A., Hong, K.-L., & Huang, C.-T. (2018). Enhancing the efficiency of the Pichia pastoris AOX1 promoter via the synthetic positive feedback circuit of transcription factor Mxr1. BMC Biotechnology, 18(1), 81. https://doi.org/10.1186/s12896-018-0492-4
• Claes, K., Van Herpe, D., Vanluchene, R., Roels, C., Van Moer, B., Wyseure, E., Vandewalle, K., Eeckhaut, H., Yilmaz, S., Vanmarcke, S., Çıtak, E., Fijalkowska, D., Grootaert, H., Lonigro, C., Meuris, L., Michielsen, G., Naessens, J., van Schie, L., De Rycke, R., … Callewaert, N. (2024). OPENPichia: Licence-free Komagataella phaffii chassis strains and toolkit for protein expression. Nature Microbiology, 9(3), 864–876. https://doi.org/10.1038/s41564-023-01574-w
• De, S., Mattanovich, D., Ferrer, P., & Gasser, B. (2021). Established tools and emerging trends for the production of recombinant proteins and metabolites in Pichia pastoris. Essays in Biochemistry, 65(2), 293–307. https://doi.org/10.1042/EBC20200138
• Irani, Z. A., Kerkhoven, E. J., Shojaosadati, S. A., & Nielsen, J. (2016). Genome-scale metabolic model of Pichia pastoris with native and humanized glycosylation of recombinant proteins. Biotechnology and Bioengineering, 113(5), 961–969. https://doi.org/10.1002/bit.25863
• Vogl, T., Fischer, J. E., Hyden, P., Wasmayer, R., Sturmberger, L., & Glieder, A. (2020). Orthologous promoters from related methylotrophic yeasts surpass expression of endogenous promoters of Pichia pastoris. AMB Express, 10, 38. https://doi.org/10.1186/s13568-020-00972-1
• Vogl, T., Sturmberger, L., Kickenweiz, T., Wasmayer, R., Schmid, C., Hatzl, A.-M., Gerstmann, M. A., Pitzer, J., Wagner, M., Thallinger, G. G., Geier, M., & Glieder, A. (2016). A Toolbox of Diverse Promoters Related to Methanol Utilization: Functionally Verified Parts for Heterologous Pathway Expression in Pichia pastoris. ACS Synthetic Biology, 5(2), 172–186. https://doi.org/10.1021/acssynbio.5b00199